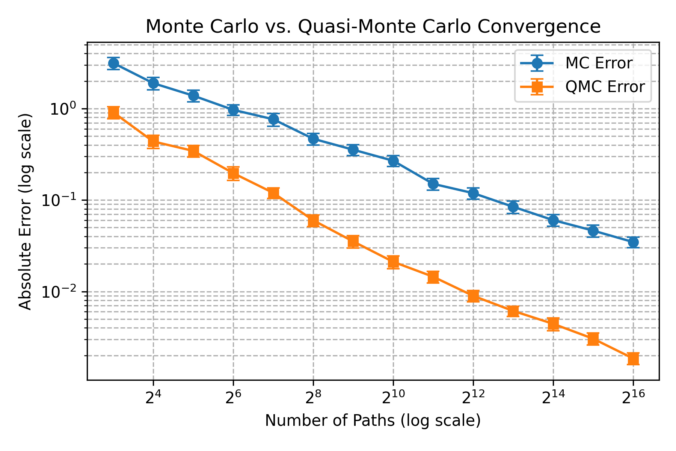
In this post, we discuss the usefulness of low-discrepancy sequences (LDS) in finance, particularly for option pricing. Unlike purely random sampling, LDS methods generate points that are more evenly distributed over the sample space. This uniformity reduces the gaps and clustering seen in standard Monte Carlo (MC) sampling and improves convergence in numerical integration problems.
A key measure of sampling quality is discrepancy, which quantifies how evenly a set of points covers the space. Low-discrepancy sequences minimize this discrepancy, leading to faster convergence in high-dimensional simulations.
Continue reading