When building trading strategies, a crucial decision is how to translate market information into trading actions.
Traditional supervised learning approaches tackle this by predicting price movements directly, essentially guessing if the price will move up or down.
Typically, we decide on labels in supervised learning by asking something like: “Will the price rise next week?” or “Will it increase more than 2% over the next few days?” While these are intuitive choices, they often seem arbitrarily tweaked and overlook the real implications on trading strategies. Choices like these silently influence trading frequency, transaction costs, risk exposure, and strategy performance, without clearly tying these outcomes to specific label modeling decisions. There’s a gap here between the supervised learning stage (forecasting) and the actual trading decisions, which resemble reinforcement learning actions.
In this post, I present a straightforward yet rigorous solution that bridges this gap, by formulating label selection itself as an optimization problem. Instead of guessing or relying on intuition, labels are derived from explicitly optimizing a defined trading performance objective -like returns or Sharpe ratio- while respecting realistic constraints such as transaction costs or position limits. The result is labeling that is no longer arbitrary, but transparently optimal and directly tied to trading performance.
Optimal Labeling as an Optimization Problem
The key insight is that labels should reflect trading decisions, since ultimately, that’s what they will drive. Instead of arbitrary thresholds, we explicitly optimize labels. This includes the ability to enforce constraints on positions, maximum leverage, and/or transaction costs. It also means we choose labels that directly maximize our desired metric -such as cumulative returns or Sharpe ratio-. By doing so, we remove guesswork from the labeling process.
Connection to Reinforcement Learning
Interestingly, this optimized labeling approach bridges supervised learning and reinforcement learning (RL). Supervised learning typically predicts static targets (like prices), while RL explicitly optimizes actions. With optimized labels, supervised learning effectively moves closer to RL…
Labels are actions chosen through optimization, directly connected to trading performance metrics. This gives our models a strong interpretability advantage, as the labels themselves represent optimized trade decisions, not just abstract forecasts.
Solving the Label Optimization
This labeling task usually involves complex performance metrics and constraints, making it difficult or impossible to compute gradients analytically. Therefore, methods like Differential Evolution (DE)—a powerful evolutionary optimization strategy introduced in the 1990s—are an ideal fit. DE explores many candidate solutions simultaneously, does not require gradients, and easily handles complex constraints. This makes it perfectly suited to our problem of optimizing labels for realistic trading strategies.
Finding optimal labels is however still active reasearch on our end. DE is slow and we are experimenting in two directions, with mixed results:
- local methods that optimize short price sequences instead of a full optimisation
- pre-trained neural network models that are trained to do (near) optimal labeling in one shot, without a search.
Types of Constraints
In practice, we impose various realistic constraints when defining optimal labels. Common examples include:
- Long-only constraints: Positions restricted to positive (long) holdings only.
- Daily volume limits: Restricting daily position changes to prevent excessive turnover and transaction costs.
- Minimum holding periods: For example, limiting trades to at least a certain number of days apart.
- Integer or fractional positions: Positions might be fractional or limited to whole units, affecting rebalancing frequency and transaction feasibility.
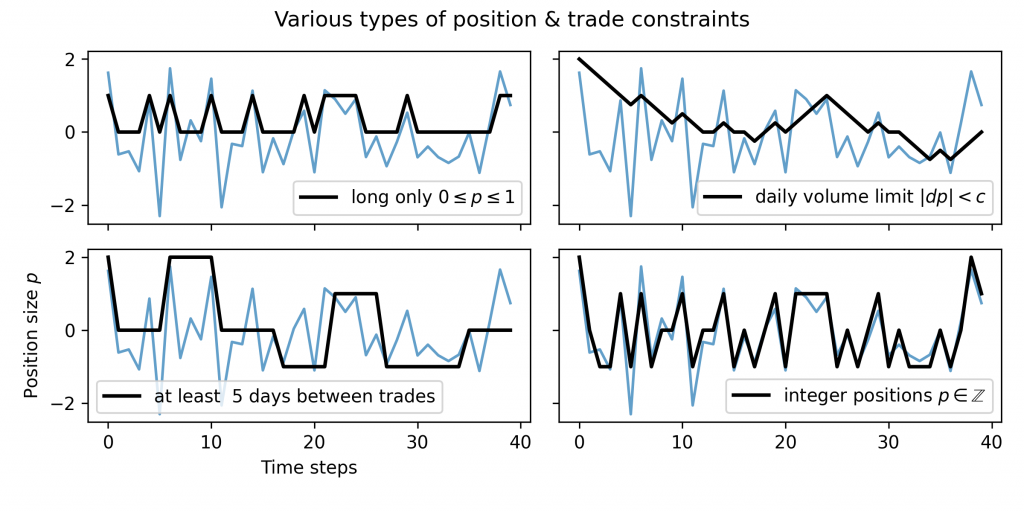
Figure 1 illustrates some of these constraints. The blue lines represent unconstrained, hypothetical positions over time, while the black lines show realistic constrained solutions. Constraints can drastically alter the shape of positions through time, reflecting practical considerations such as transaction costs, daily volume limits, trading frequency limits, and trade position size constraints.
Types of Optimization Targets
The choice of the optimization target -often called the loss or objective function- is also important. Different targets lead to different labeling outcomes and thus different trading strategies. Common examples include:
- Maximizing returns: Focuses purely on profitability, regardless of volatility.
- Maximizing Sharpe ratio: Balances return against risk, rewarding consistency and penalizing volatility.
- Including transaction costs explicitly: Directly penalizes frequent trading and excessive turnover.
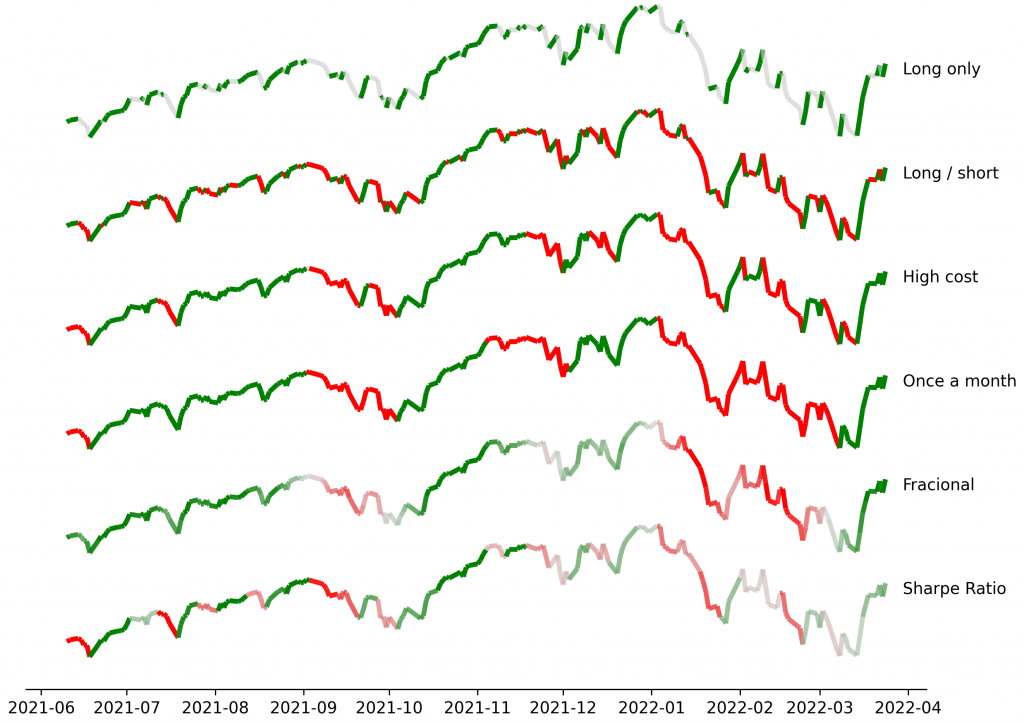
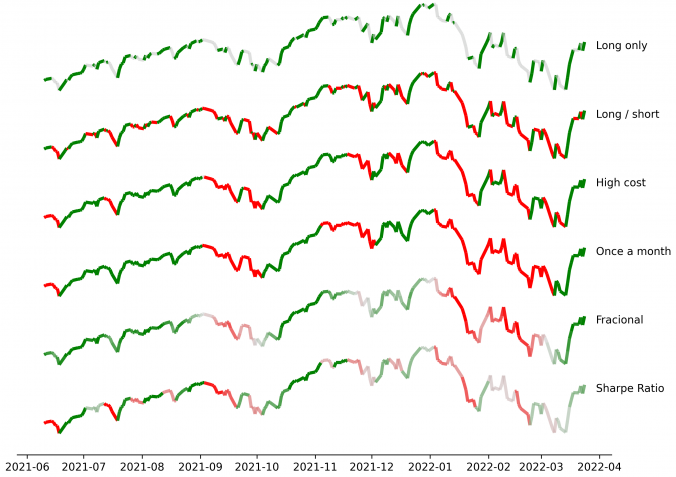
Figure 2 shows how selecting different optimization targets significantly affects optimal labeling. Green segments indicate target (long) positions, red segments indicate short positions, and grey segments indicate periods of neutrality or inactivity.