In the previous post, we built a simple gravitational lens raytracer that simulates how an image would be distorted when seen through a point-mass gravitational lens. That approach was fully numerical: we traced rays from each pixel and observed how they bent. But if we’re working with small, elliptical galaxies and want to understand how their shapes change statistically, we can use an analytical model based on the lensing Jacobian.

Comparing Raytracer and Analytical Jacobian

Below we show a visual comparison of the two approaches:

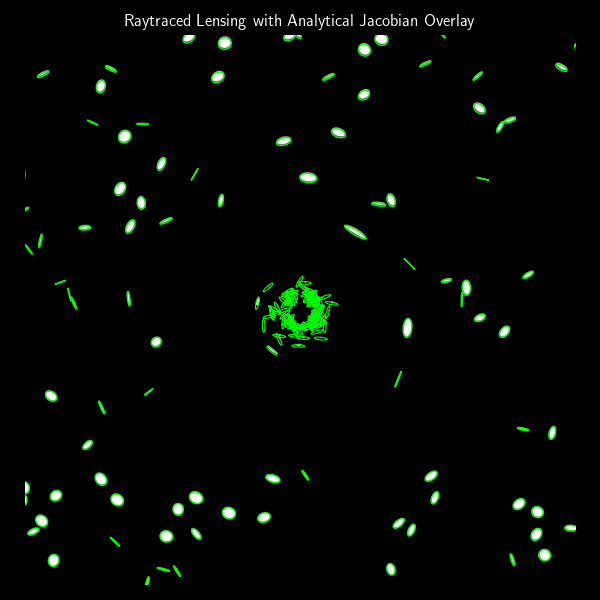
  • White ellipses: raytraced shapes using our numerical simulator from the previous post.
  • Green outlines: analytical predictions using the Jacobian method introduced here.

The match is near-perfect in terms of location, orientation, and ellipticity, which validates both methods. However, the analytical approach assumes each galaxy is infinitesimally small. It can’t capture bending across extended galaxies (e.g., arcs), but this can be approximated by modeling large galaxies as clusters of smaller ones.

The Analytical Method

We start from the gravitational lens equation for a point mass and derive expressions for both the inverse mapping and the Jacobian matrix, which describes how a small patch (or galaxy) is deformed by the lens.

Finding the Lensed Positions

In gravitational lensing, we relate the angular position of the source \vec{\beta} to the observed position of the image(s) \vec{\theta} via the lens equation:

    \[\vec{\beta} = \vec{\theta} - \vec{\alpha}(\vec{\theta})\]

For a point mass lens, the deflection angle \vec{\alpha} is radial and given by:

    \[\vec{\alpha}(\vec{\theta}) = \frac{C}{|\vec{\theta} - \vec{\theta}_L|^2} (\vec{\theta} - \vec{\theta}_L)\]

Here C is a constant that includes mass and geometric factors, and \vec{\theta}_L is the angular position of the lens center.

This equation generally has two solutions \vec{\theta}+ and \vec{\theta}- corresponding to light rays passing on either side of the lens. These are the two images we observe of the same background source.

We can compute these solutions explicitly using the quadratic form of the lens equation:

    \[\theta = \frac{\beta \pm \sqrt{\beta^2 + 4C}}{2}\]

and rescale it back to 2D pixel space:

def lens_inverse(source_pos, lens_center, C):
    """
    Compute the two image positions from a single source position using the inverse lens equation.

    Parameters:
        source_pos (tuple): (x, y) position of the source galaxy in pixels.
        lens_center (tuple): (x, y) position of the lens center in pixels.
        C (float): Lens strength constant (proportional to mass).

    Returns:
        theta_plus, theta_minus: Two image positions as (x, y) tuples.
    """
    dx = source_pos[0] - lens_center[0]
    dy = source_pos[1] - lens_center[1]
    beta = np.sqrt(dx**2 + dy**2)

    if beta < 1e-9:
        theta_E = np.sqrt(C)
        return [lens_center[0] + theta_E, lens_center[1]], [lens_center[0] - theta_E, lens_center[1]]

    theta_mag = (beta + np.sqrt(beta**2 + 4 * C)) / 2
    theta_sign = (beta - np.sqrt(beta**2 + 4 * C)) / 2
    dx_unit = dx / beta
    dy_unit = dy / beta

    theta_plus = [lens_center[0] + dx_unit * theta_mag, lens_center[1] + dy_unit * theta_mag]
    theta_minus = [lens_center[0] + dx_unit * theta_sign, lens_center[1] + dy_unit * theta_sign]
    return theta_plus, theta_minus

The Lensing Jacobian

The Jacobian matrix describes how small displacements in the image plane get mapped to displacements in the source plane. It’s essentially the derivative of the lens equation:

    \[\mathbf{J}(\vec{\theta}) = \frac{\partial \vec{\beta}}{\partial \vec{\theta}} = \mathbf{I} - \frac{\partial \vec{\alpha}}{\partial \vec{\theta}}\]

We use this matrix to model how a small elliptical galaxy is stretched and sheared.

For a point mass lens, this derivative is known analytically:

def lens_jacobian(theta, lens_center, C):
    """
    Compute the Jacobian matrix of the lens mapping at one or more image positions.

    Parameters:
        theta (np.ndarray): N x 2 array of image positions (x, y).
        lens_center (tuple): (x, y) position of the lens.
        C (float): Lens strength constant.

    Returns:
        N x 2 x 2 array of Jacobian matrices.
    """
    dx = theta[:, 0] - lens_center[0]
    dy = theta[:, 1] - lens_center[1]
    r2 = dx**2 + dy**2 + 1e-9
    r4 = r2**2
    fac = C / r4

    d11 = 1 - fac * (dy**2 - dx**2)
    d22 = 1 + fac * (dy**2 - dx**2)
    d12 = d21 = 2 * fac * dx * dy

    return np.stack([d11, d12, d21, d22], axis=1).reshape(-1, 2, 2)

This matrix tells us how much each galaxy is stretched and rotated at its lensed position.

Deforming an Ellipse

To model how a small elliptical galaxy is affected, we start with its shape matrix \mathbf{S}:

    \[\mathbf{S} = \mathbf{R}(\phi) \begin{bmatrix} a & 0 \ 0 & b \end{bmatrix} \mathbf{R}^T(\phi)\]

where a, b are the semi-axes and \phi the orientation. Then we apply the inverse Jacobian:

    \[\mathbf{A} = \mathbf{J}^{-1} \cdot \mathbf{S}\]

We extract the new shape parameters from \mathbf{A} using singular value decomposition (SVD).

def ellipse_params_from_jacobian(J, a_arr, b_arr, angle_arr, sort_axes=False):
    """
    Apply the Jacobian transformation to ellipse parameters and return the lensed semi-axes and angle.

    Parameters:
        J (np.ndarray): N x 2 x 2 array of Jacobians.
        a_arr (np.ndarray): Array of semi-major axes.
        b_arr (np.ndarray): Array of semi-minor axes.
        angle_arr (np.ndarray): Array of orientation angles in degrees.
        sort_axes (bool): Whether to ensure a >= b in output.

    Returns:
        List of (a, b, angle) tuples for each lensed ellipse.
    """
    N = J.shape[0]
    ellipses = []
    for i in range(N):
        phi = np.radians(angle_arr[i])
        R = np.array([[np.cos(phi), -np.sin(phi)],
                      [np.sin(phi),  np.cos(phi)]])
        S = R @ np.diag([a_arr[i], b_arr[i]]) @ R.T
        A = np.linalg.inv(J[i]) @ S
        U, s, _ = np.linalg.svd(A)

        a, b = s[0], s[1]
        angle = np.degrees(np.arctan2(U[1, 0], U[0, 0])) % 180

        if sort_axes and b > a:
            a, b = b, a
            angle = (angle + 90) % 180

        ellipses.append((a, b, angle))
    return ellipses

This routine rotates each ellipse to its original orientation, applies the inverse Jacobian to the shape matrix, and performs SVD to recover the new axes and orientation.

Wrapup

These equations and code compute how galaxies are statistically stretched and rotated by a gravitational lens. This is useful because it allows us to easily simulate distributions for shape, ellipticity, and orientation and how these deform in the presense of a gravitational lens. Aditionally, we can also use these equations for likelihood modelling, -e.g. to compute if it’s likely that there is a (weak)lens somewhere in an image-.