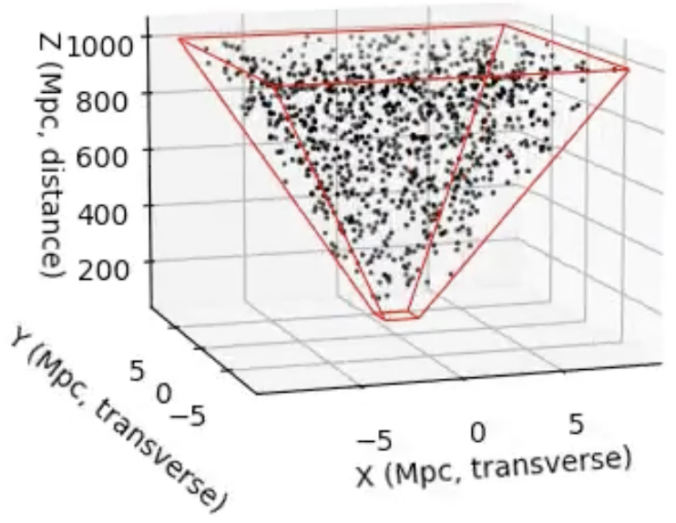
How to Sample the 3D Universe You See in an Image – SITMO Machine Learning

When we look at an astronomical image, we see a 2D projection of a 3D universe. But suppose we want to simulate the distribution of galaxies behind that image, for example, to generate synthetic data, test detection algorithms, or check if real galaxy distributions statistically deviate from what we’d expect under uniformity. To do this, we need a way to sample galaxies uniformly in 3D space, restricted to the cone of space visible in an image.

This post shows how to do that, using a rectangular patch of sky (like what you might get from a telescope image), and a minimum and maximum depth. The result is a cloud of galaxy positions in 3D, uniformly spread through the volume that the image captures. This synthetic distribution can serve as a null hypothesis: if real data shows patterns that deviate from this, we might be seeing lensing, clustering, or other cosmic structure.

The Sampling Problem

Suppose the image spans an angular width $w$ and height $h$ , in radians, and we’re interested in galaxies between distances $r_\text{min}$ and $r_\text{max}$ away from us. We want to draw $N$ galaxy positions $(x_i, y_i, z_i)$ uniformly from the corresponding 3D volume.

We assume that the angular patch is small, so we can use the small-angle approximation. The visible volume is then approximately a rectangular cone: its cross-section expands linearly with distance, and its depth is from $r_\text{min}$ to $r_\text{max}$ .

To sample uniformly in this volume, we proceed in three steps:

Sample radius $r$ such that the probability density is uniform in volume (not uniform in radius). This means sampling $r$ from:

$r = \left( u (r_\text{max}^3 - r_\text{min}^3) + r_\text{min}^3 \right)^{1/3} \\\quad \text{where } u \sim \mathcal{U}(0,1)$

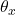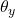Sample angular offsets $\theta_x$ and $\theta_y$ uniformly in the rectangular patch:

$\theta_x \sim \mathcal{U}\left( -\frac{w}{2}, \frac{w}{2} \right), \quad \theta_y \sim \mathcal{U}\left( -\frac{h}{2}, \frac{h}{2} \right)$

Convert spherical coordinates to Cartesian coordinates. For small angles, we use:

$x = r \theta_x, \quad y = r \theta_y, \quad z = r$

This gives a galaxy distribution that is uniform in 3D space within the volume seen by the camera.

Projecting to the Image Plane

To visualize the galaxy distribution from the observer’s point of view, we project the 3D coordinates onto a 2D image. This is essentially the inverse of the process used to sample the angular directions.

For small angles, the angular displacement on the sky is simply:

$x_\text{img} = \frac{x}{z}, \quad y_\text{img} = \frac{y}{z}$

This maps each galaxy to a position on the image plane in radians. The next plot show the 2D image projection of a the 3D random samples. At each location we’ve place a randomly oriented circle as a simple galaxy model.

Code Implementation

Here’s the full implementation in Python:

def sample_galaxies_rectangular_patch(
    N,
    width_deg=1.0,
    height_deg=1.0,
    r_min=100.0,
    r_max=1000.0,
    seed=None
):
    """
    Sample galaxies uniformly in 3D space inside a rectangular angular patch.

    Parameters
    ----------
    N : int
        Number of galaxies to sample.
    width_deg : float
        Width of angular patch in degrees (RA-like direction).
    height_deg : float
        Height of angular patch in degrees (Dec-like direction).
    r_min : float
        Minimum distance from observer in Mpc.
    r_max : float
        Maximum distance from observer in Mpc.
    seed : int or None
        Random seed.

    Returns
    -------
    x, y, z : np.ndarray
        Cartesian coordinates of sampled galaxies in Mpc.
    """
    if seed is not None:
        np.random.seed(seed)

    # Sample depth uniformly in volume
    u = np.random.uniform(0, 1, N)
    r = (u * (r_max**3 - r_min**3) + r_min**3) ** (1/3)

    # Convert angular width/height to radians
    width_rad = np.radians(width_deg)
    height_rad = np.radians(height_deg)

    # Sample theta_x and theta_y uniformly
    theta_x = np.random.uniform(-width_rad / 2, width_rad / 2, N)
    theta_y = np.random.uniform(-height_rad / 2, height_rad / 2, N)

    # Project into Cartesian coordinates using small-angle approximation
    x = r * theta_x
    y = r * theta_y
    z = r

    info = {
        'width_deg': width_deg, 
        'height_deg': height_deg, 
        'r_min': r_min, 
        'r_max': r_max, 
        'theta_x': theta_x, 
        'theta_y': theta_y
    }

    return x, y, z, info

def project_to_image_plane(x, y, z):
    """
    Project 3D Cartesian galaxy coordinates into 2D image plane using perspective projection.

    Parameters
    ----------
    x, y, z : np.ndarray
        Galaxy positions in Mpc.

    Returns
    -------
    x_img, y_img, z : np.ndarray
        Projected 2D image positions (in radians), and preserved z (depth).
    """
    # Compute angular position as seen from the origin (observer)
    x_img = x / z  # small angle approximation: tan(theta) ≈ theta
    y_img = y / z
    return x_img, y_img

This is the simplest possible version, ideal for testing lensing estimators or simulating null models. More realistic models might account for galaxy luminosity functions or clustering, but uniform sampling is where we begin.