Imagine you’re comparing two trading strategies. One has made a handful of successful trades over the past month, while the other shows a different success pattern over a slightly shorter period. Both show promise, but which one truly performs better? And more importantly, how confident can we be in that judgment, given such limited data?

To explore this, let’s turn to a simpler but mathematically equivalent situation: comparing two coins. The first coin is flipped 10 times and lands heads 3 times. The second coin is flipped 9 times and lands heads 5 times. We want to know: what is the probability that the second coin has a higher chance of landing heads than the first?

This question can be approached using Bayesian statistics. When we observe ( k ) heads in ( n ) coin tosses, the probability distribution for the true probability of heads -given what we know- is given by the Beta distribution:

    \[\text{Beta}(\alpha = k + 1, \, \beta = n - k + 1)\]

Using this, we can model the two coins’ head probabilities with the following Beta distributions:

  • First coin: \text{Beta}(3+1, \, 10-3+1) = \text{Beta}(4, 8)
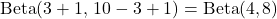
  • Second coin: \text{Beta}(5+1, \, 9-5+1) = \text{Beta}(6, 5)

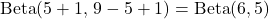
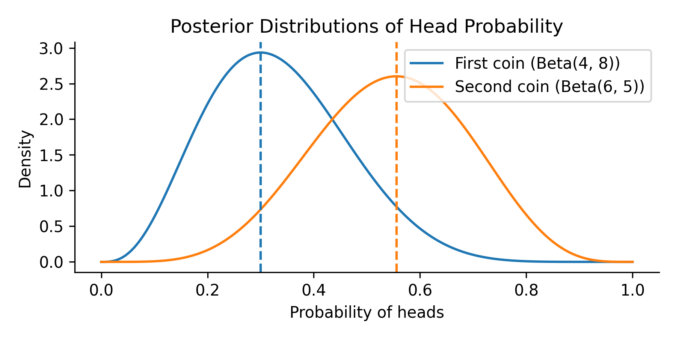
These distributions are visualized below:

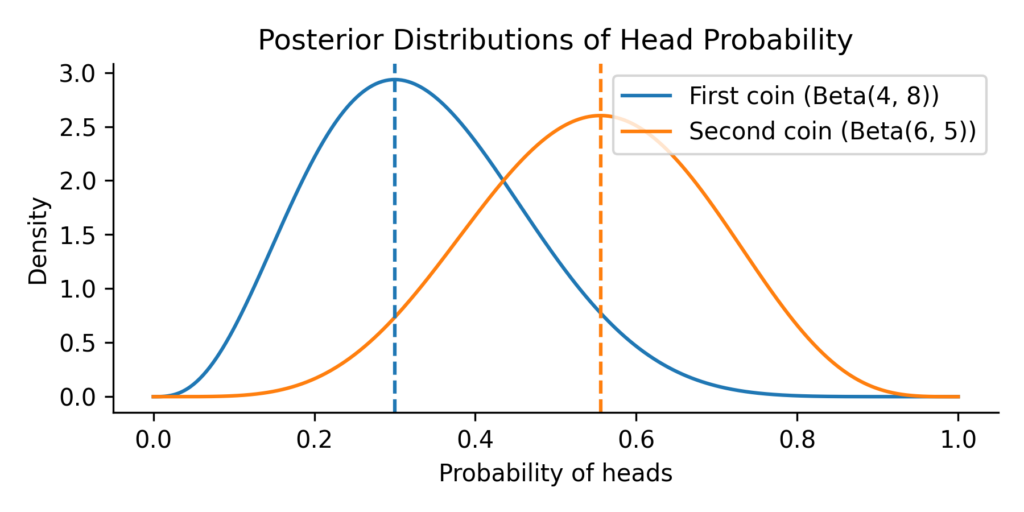
The plot above shows the uncertainty around each coin’s probability of landing heads, given the limited number of tosses. We now want to compute the probability that a sample from the second coin’s distribution is greater than a sample from the first coin’s distribution. Formally, we want:

    \[P(X > Y), \quad \text{where } X \sim \text{Beta}(6, 5), \, Y \sim \text{Beta}(4, 8)\]

This problem is not trivial and does not have a simple closed-form solution. However, in the paper “Exact Calculation of Beta Inequalities” by John D. Cook, a numerical algorithm is provided that allows for precise computation of this probability. Such calculations are common in Bayesian A/B testing and clinical trials, where we want to know which of two treatments performs better based on limited evidence.

Below is a Python implementation of this algorithm. The function PrBeta1GtBeta2(a1, b1, a2, b2) computes the probability that a sample from \text{Beta}(a_1, b_1) is greater than a sample from \text{Beta}(a_2, b_2).

In our case, we call:

PrBeta1GtBeta2(6, 5, 4, 8)

This returns approximately 0.858, or 85.8%. So, based on the available data, there is an 85.8% chance that the second coin has a higher probability of landing heads than the first.

import numpy as np
from scipy.special import gammaln

def PrBeta1GtBeta2(a1, b1, a2, b2):
    def h_abcd_ln(a1, b1, a2, b2):
        return (gammaln(a1 + a2) + gammaln(b1 + b2) + gammaln(a1 + b1) + gammaln(a2 + b2)
                - gammaln(a1) - gammaln(b1) - gammaln(a2) - gammaln(b2) 
                - gammaln(a1 + b1 + a2 + b2))
    
    def g_aba2_ln(a1, b1, a2):
        return (gammaln(a1 + b1) + gammaln(a1 + a2)
                - gammaln(a1 + b1 + a2) - gammaln(a1))
    
    def g_abcd_via_d(a1, b1, a2, b2):
        x = np.exp(g_aba2_ln(a1, b1, a2))
        for i in range(2, int(b2) + 1):
            x += np.exp(h_abcd_ln(a1, b1, a2, i - 1)) / (i - 1)
        return x

    m = min(a1, b1, a2, b2)
    if m == a1:
        return g_abcd_via_d(b2, a2, b1, a1)
    elif m == b1:
        return 1 - g_abcd_via_d(a2, b2, a1, b1)
    elif m == a2:
        return 1 - g_abcd_via_d(b1, b2, a1, a2)
    elif m == b2:
        return g_abcd_via_d(a1, b1, a2, b2)

Bibliography

Cook, John D.,Exact Calculation of Beta Inequalities
UT MD Anderson Cancer Center Department of Biostatistics Working Paper Series, 2005