In some cases, we need to construct a correlation matrix with a predefined set of eigenvalues, which is not trivial since arbitrary symmetric matrices with a given set of eigenvalues may not satisfy correlation constraints (e.g., unit diagonal elements).
A practical method to generate such matrices is based on the Method of Alternating Projections (MAP), as introduced by Waller (2018). This approach iteratively adjusts a matrix between two sets until convergence. It goes like this:
- Normalize the eigenvalues:
- Ensure they are sorted in descending order.
- Scale them such that their sum equals
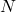 , the matrix size.
, the matrix size.
- Generate a random orthonormal matrix:
- Construct a random matrix.
- Perform QR decomposition to obtain the orthonormal matrix.
- Iterate until convergence:
- Construct an symmetric positive definite (SPD) matrix using the target eigenvalues and the random orthonormal matrix:
- Clamp values between
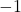 and
and 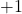 to maintain correlation constraints.
to maintain correlation constraints. - Force all elements on the diagonal to be
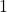 .
.
- Clamp values between
- Perform eigen decomposition to extract new eigenvalues and eigenvectors.
- Replace the computed eigenvalues with the target values.
- Compute the distance measure .
- Stop if the distance measure is below a given tolerance.
- Construct an symmetric positive definite (SPD) matrix using the target eigenvalues and the random orthonormal matrix:
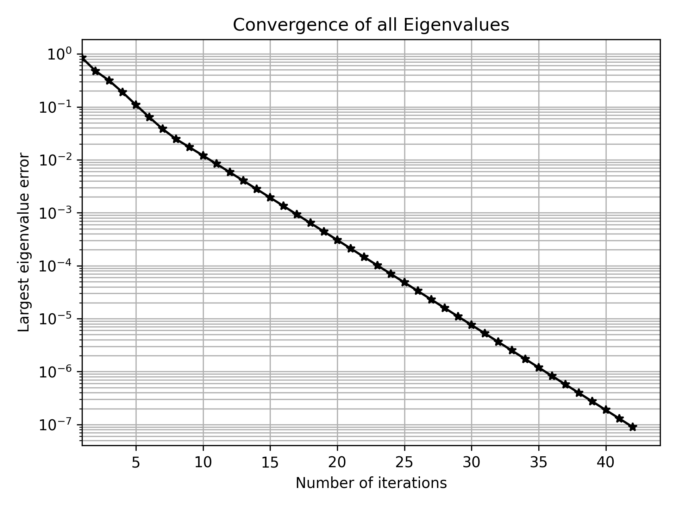
The algorithm seems to converge exponentially fast:
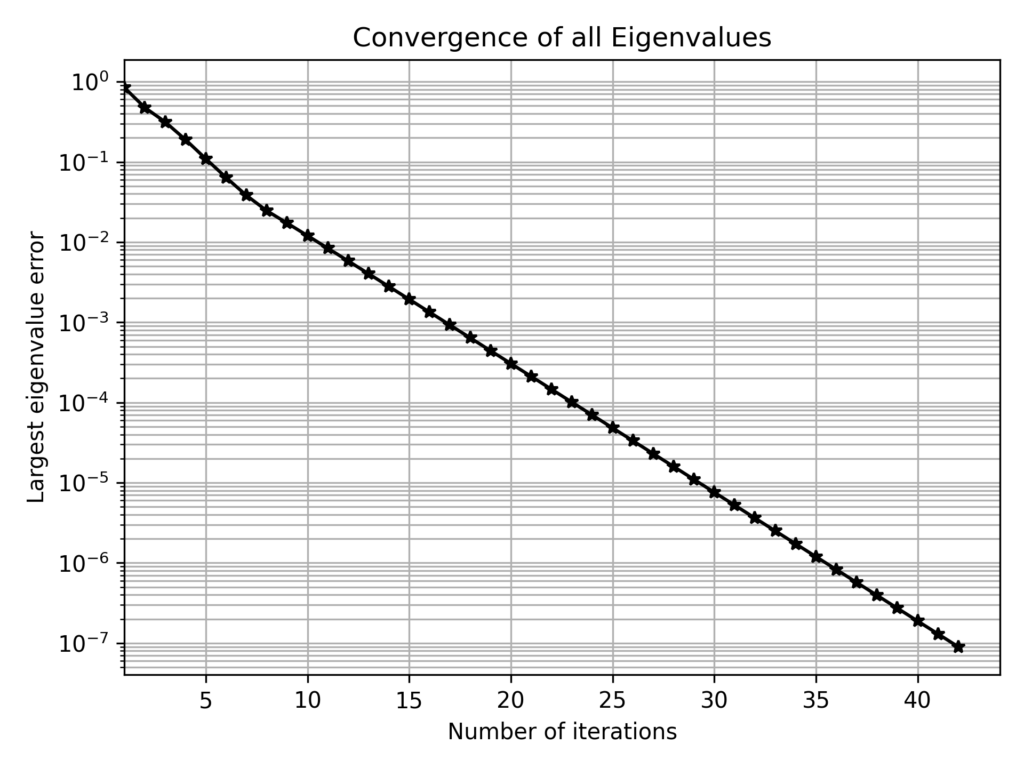
Below Python code!
import numpy as np
def eig_to_cor(eigen_values, eigen_vectors):
"""
Construct a correlation matrix from given eigenvalues and eigenvectors.
"""
cor = eigen_vectors @ np.diag(eigen_values) @ eigen_vectors.T
cor = np.clip(cor, -1, 1) # Ensure valid correlation values
np.fill_diagonal(cor, 1.0) # Force unit diagonal elements
return cor
def cor_to_eig(cor):
"""
Extract eigenvalues and eigenvectors from a correlation matrix,
ensuring they are sorted in descending order.
"""
eigen_values, eigen_vectors = np.linalg.eigh(cor)
idx = eigen_values.argsort()[::-1]
return eigen_values[idx].real, eigen_vectors[:, idx].real
def random_orthonormal_matrix(n):
"""
Generate a random nxn orthonormal matrix using QR decomposition.
"""
Q, _ = np.linalg.qr(np.random.randn(n, n))
return Q
def normalize_eigen_values(eigen_values):
"""
Normalize eigenvalues to sum to the matrix dimension (n) and ensure that they are sorted in descending order.
"""
eigen_values = np.sort(eigen_values)[::-1] # Ensure descending order
return len(eigen_values) * eigen_values / np.sum(eigen_values)
def gen_cor_with_eigenvalues(eigen_values, tol=1E-7):
"""
Generate a correlation matrix with the specified eigenvalues
using the Method of Alternating Projections.
"""
target_eigen_values = normalize_eigen_values(eigen_values)
eigen_vectors = random_orthonormal_matrix(len(target_eigen_values))
while True:
cor = eig_to_cor(target_eigen_values, eigen_vectors)
eigen_values, eigen_vectors = cor_to_eig(cor)
if np.max(np.abs(target_eigen_values - eigen_values)) < tol:
break
return cor
# Example usage:
cor_matrix = gen_cor_with_eigenvalues([3, 1, 1/3, 1/3, 1/3])
print(cor_matrix)
>
array([[ 1. , 0.52919521, -0.32145437, -0.45812423, -0.65954354],
[ 0.52919521, 1. , -0.61037909, -0.65821403, -0.46442884],
[-0.32145437, -0.61037909, 1. , 0.64519865, 0.23287104],
[-0.45812423, -0.65821403, 0.64519865, 1. , 0.38261988],
[-0.65954354, -0.46442884, 0.23287104, 0.38261988, 1. ]])
Waller, N. G. (2018). Generating Correlation Matrices With Specified Eigenvalues Using the Method of Alternating Projections. The American Statistician, 74(1), 21–28. https://doi.org/10.1080/00031305.2017.1401960